Clicando no link a seguir AQUI, você vai acessar um simples applet java que simula um fluido (líquido, gás, sólido, depende da temperatura e pressão que você escolher) composto por discos macios.
É como se a gente estivesse observando uma caixa contendo partículas atômicas (argônio, xenônio, etc) só que apenas em duas dimensões.
Dá para usar esse programinha em uma aula de físico-química para ensinar sobre estados termodinâmicos da matéria apenas variando os valores das variáveis de estado (temperatura, densidade, pressão, número de átomos, etc).
<Dr. Chatoff mode on>
Apenas a título de informação, essa técnica de modelagem molecular é bem comum no meio acadêmico. Eu mesmo a conheço bem, visto que fiz doutorado em simulação de líquidos por dinâmica molecular. As partículas resumem-se a bolinhas que interagem umas com as outras por meio de potenciais aditivos aos pares, no caso desse applet usa-se o potencial de Lennard-Jones 12-6.
![V(r) = 4\epsilon \left[ \left(\frac{\sigma}{r}\right)^{12} - \left(\frac{\sigma}{r}\right)^{6} \right],](http://upload.wikimedia.org/math/3/2/2/322cc39097022640ec80fb402803e4c0.png)
Na equação acima, o parâmetro ε representa toda a parte eletrônica e nuclear do átomo, é chamado de parâmetro energético, polarizabilidade ou simplesmente "profundidade do poço de potencial". O parâmetro σ representa a distância entre dois átomos do mesmo tipo na qual a energia potencial é zero. Representa o tamanho do átomo, tem valores grandes para átomos grandes (xenônio, por exemplo) e valores pequenos para átomos pequenos (hélio, por exemplo).
O parâmetro r representa a distância de separação entre os dois átomos. Se r for muito pequeno, o ramo de energia potencial repulsiva r−12 cresce absurdamente e as partículas tenderão a se repelir, se a distância r tornar-se muito grande, o ramo de energia potencial atrativa r−6 vai assumir maior valor e fazer com que as partículas voltem a se aproximar. Isso ajuda a representar as famosas forças de dispersão, conhecidas na Química como forças de Van der Waals.
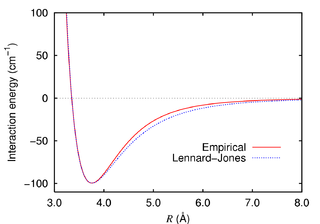
A figura acima, roubada descaradamente da Wikipedia, mostra a forma da função de potencial para um dímero de argônio (dímero significa um par de átomos se atraindo e se repelindo). As partículas se movem usando-se uma série de equaçõíes desenvolvidas há muito tempo pelo Sr. Isaac Newton, aquelas mesmas que a gente estuda no ensino médio (F=m.a, lembram?).A força da equação acima vem de um truque matemático. A função de potencial de Lennard-Jones passa por uma operação matemática conhecida por derivada e fornece a força entre duas partículas separadas por uma distância r. Com a força em mãos, pode-se calcular a nova posição das partículas, calcula-se a nova força entre as duas partículas, obtém-se uma nova posição e por aí vai. Isso tudo é chamado de equações de movimento. No caso do applet da dica do dia, o algoritmo usado é o de Verlet. <Dr. chatoff mode off>
Agora, voltando ao applet:
Escolha um conjunto de parâmetros (número de átomos, tamanho dos átomos, passo temporal e velocidade da animação - ambos têm a ver com as equações de movimento) e observe como as partículas saem de uma situação de ordem perfeita para uma situação de bagunça absoluta em pouquíssimo tempo.
Se você achar que a coisa acontece rápido demais, pode usar o botão "slower" para observar a coisa com mais calma.
Além disso, por mais lento que você faça a simulação acontecer, lembre-se que tudo acontece na escala dos femtossegundos (algo em torno de 0,000000000000001 segundos). Em outras palavras, muuuuuuuuuiiito rápido mesmo.
É claro que esse tipo de simulação pode se tornar muito mais complicada do que o mostrado nesse applet.
Na indústria farmacêutica é comum usar-se softwares mais complexos para investigar a interação de possíveis fármacos com sítios catalíticos de enzimas humanas ou de outros seres vivos. A utilidade disso é desenvolver novos medicamentos a um custo muito baixo.
Além disso, teorias sobre o estado líquido da matéria são desenvolvidas com o auxílio desses softwares.
Dá para aprender coisas bem legais com a DM (ou MD, na sigla em inglês - de Molecular Dynamics), e assim que for possível eu vou postar exemplos mais concretos aqui no blog.
Peço desculpas aos leitores ocasionais pelo post mais técnico que o normal, mas me deu vontade de escrever sobre isso. :)
P.S.: Esqueci de colocar o link para o applet, mas agora já está corrigido. Divirtam-se.
